CBSE Class 12 Maths Chapter 7 Integrals Revision Notes: Download PDF

CBSE Class 12 Mathematics Chapter 7 Integrals Revision Notes: With the 2023 board exams around the corner, it’s time to put down the books and start the exam preparations. Mathematics is a subject that requires substantial practice and thorough revision. In the final stage of the academic year, students are advised to focus on revision rather than taking up new concepts to learn.

The CBSE Class 12 board exams are set to start from February 15, 2024, and the mathematics paper will be held on March 9. The seventh chapter in the Class 12 math books is Integrals. It’s one of the most important and significant chapters in the curriculum as part of the calculus section.

You can check out the CBSE Class 12 Chapter 7 Integrals revision notes here, along with additional study resources like mind maps and multiple-choice questions.

CBSE Class 12 Maths Chapter 7 Integrals Revision Notes

Basic Definitions, Summary and Formulas

Integration

In differential calculus, we are given a function and we have to find the derivative or differential of this function, but in integral calculus, we are to find a function whose differential is given. Thus, integration is a process which is the inverse of differentiation.

These integrals are called indefinite integrals or general integrals, C is called constant of integration. All these integrals differ by a constant.

Definite Integrals

A definite integral is the area under a curve between two fixed limits.

A definite integral is denoted by _a∫^b ƒ(x)dx, where a is called the lower limit of the integral and b is called the upper limit of the integral.

The definite integral is introduced either as the limit of a sum or if it has an anti derivative F in the interval [a, b], then its value is the difference between the values of F at the end points, i.e., F(b) – F(a).

Properties of Definite Integrals

Evaluation of Definite Integrals by Substitution

In the previous sections, we have discussed several methods for finding the indefinite integral. One of the important methods for finding the indefinite integral is the method of substitution.

To evaluate  _a∫^b ƒ(x)dx, by substitution, the steps could be as follows:

1. Consider the integral without limits and substitute, y = f (x)or x = g(y) to reduce the given integral to a known form.
2. Integrate the new integrand with respect to the new variable without mentioning the constant of integration.
3. Resubstitute for the new variable and write the answer in terms of the original variable.
4. Find the values of answers obtained in (3) at the given limits of integral and find the difference of the values at the upper and lower limits.

Indefinite Integrals

An integral does not have any upper and lower limit.

First fundamental theorem of integral calculus

Let the area function be defined by A(x) =  _a∫^x ƒ(x)dx for all x ≥ a, where the function ƒ is assumed to be continuous on [a, b]. Then A′(x) = ƒ (x) for all x ∈ [a, b].

Second fundamental theorem of integral calculus

Let ƒ be a continuous function of x defined on the closed interval [a, b] and let F be another function such that d/dx F(x) = ƒ(x) for all x in the domain of ƒ, then

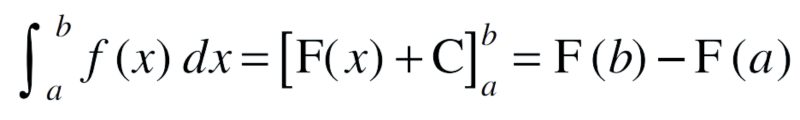
This is called the definite integral of ƒ over the range [a, b], where a and b are called the limits of integration, a being the lower limit and b the upper limit.

Standard Integrals

Integration By Substitution

A change in the variable of integration often reduces an integral to one of the fundamental integrals. The method in which we change the variable to some other variable is called the method of substitution. When the integrand involves some trigonometric functions, we use some well-known identities to find the integrals. Using the substitution technique, we obtain the following standard integrals.

(i) ∫tanxdx = log|secx|+ C

(ii) ∫cotxdx = log|sinx|+ C

(iii) ∫secxdx= log|secx + tanx|+ C

(iv) ∫cosecxdx = log|cosecx – cotx|+ C

View and download the full PDF for CBSE Class 12 Mathematics Chapter 7 Integrals Revision notes below.