Jagran Josh
Difference Between Correlation And Regression: Both Correlation And Regression are important statistical tools but Correlation is used only to check and determine association whereas Regression showcases the cause-and-effect relationship.
Correlation vs Regression: Both correlation and regression are two powerful tools of statistics and data analysis used to understand the relationships between variables. However, they serve distinct purposes and provide different insights. While correlation is used to determine the relationship between two variables, Regression is used to determine how changes in the independent variable will affect the dependent variable.
Difference Between Correlation And Regression
In this article, we will try to understand the key differences between correlation and regression with definitions, applications, major differences and examples.
What is Correlation?
Correlation indicates the relationship between two variables in strength and direction. It is used to identify relationships between two variables in fields such as economics, finance, medicine, and psychology.
In short, correlation is a statistical measure to measure association.
What is Regression?
Regression indicates or predicts the effect of change in one variable on another variable. It is used in fields such as psychology, finance, economics and medicine.
In short, regression is a statistical tool to predict outcomes.
What is the difference between Correlation and Regression?
|
Correlation produces a single value, the correlation coefficient, which quantifies the strength and direction of association. A positive correlation (close to +1) suggests a strong positive relationship, meaning that as one variable increases, the other tends to increase as well. Conversely, a negative correlation (close to -1) indicates a strong negative relationship, implying that as one variable increases, the other tends to decrease. A correlation coefficient near 0 suggests a weak or no linear relationship. A positive correlation implies that when one variable increases, the other tends to increase as well, while a negative correlation implies that when one variable increases, the other tends to decrease. |
|
Regression models the association between two variables and forecasts the dependent variable’s value using the independent variable’s value as a basis. Regression provides an equation that describes the relationship between variables, allowing for prediction and examination of causation. Regression equation is linear. |
When to Use Correlation?
Correlation is used to identify and assess the strength of the relationship between two variables.
When to Use Regression?
Regression is used to model the relationship between two variables and predict the value of one variable based on the value of the other variable.
Correlation and Regression Formula
Correlation is calculated using Pearson’s Correlation Coefficient:
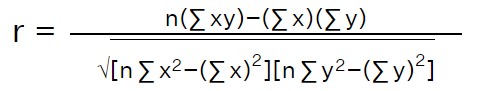
Where,
r = Pearson correlation coefficient
x = Values in the first set of data
y = Values in the second set of data
n = Total number of values
Regression is calculated using Ordinary Least Squares (OLS) Linear Regression:
Where,
Y = Dependent variable
a = [(∑y)(∑x2) – (∑x)(∑xy)]/ [n(∑x2) – (∑x)2]
b = [n(∑xy) – (∑x)(∑y)]/ [n(∑x2) – (∑x)2]
X = Independent variable
When to Use Correlation and Regression with Example
If you would like to study the relationship between screen-time and stress, you can use correlation to identify if there is any statistically significant relationship between these. Based on whether the correlation coefficient is positive or negative or zero, you can determine if they are positively associated, negatively associated or not associated at all, respectively.
If correlation proves a statistically significant relationship between stress and screen-time then you can go ahead and use regression to model the relationship between the two variables and predict the level of stress based on the amount of screen-time or vice versa.
Correlation vs Regression: Key Highlights
The following table summarises the main differences between correlation and regression:
|
Characteristic |
Correlation |
Regression |
|
Purpose |
Measures the strength and direction of the relationship between two variables. Neither it makes any predictions nor establish causations |
Models the relationship between two variables and predicts the value of the dependent variable based on the value of the independent variable |
|
Variables |
Used to create an association between two or more variables and both the variables are treated as independent variables |
Predicts outcome of the changes made on a dependent variable and the other variable(s) are treated as independent variables |
|
Output |
Correlation coefficient |
Regression equation |
|
Interpretation |
The correlation coefficient indicates the strength and direction of the relationship between the two variables. It does not address causation. |
The regression equation can be used to predict the value of the dependent variable based on the value of the independent variable(s). It can be used to explore the causation. |
|
Usage |
Association between sleep duration and stress |
Predict the level of stress (dependent variable) based on sleep duration (independent variable). |
Related:
#Difference #Correlation #Regression #Key #Dissimilarity
